2020，又一位数学大师仙逝。
7月6日，美国著名数学家葛立恒（Ronald Graham）因病逝世，享年85岁。
虽然很多数学爱好者不敢相信这个事实，但美国数学学会（AMS），已在官网发布了葛立恒的讣告：
这位曾经的AMS主席获得官网这样的评价——他是离散数学的领军人物。
与葛立恒合作过25篇论文的数学家Steve Butler也在社交媒体上证实了这一消息。
这位传奇数学家留给大众最重要的遗产，就是葛立恒数，这个数学证明中用到的最大数曾入选吉尼斯世界纪录为人熟知。
而葛立恒数仅仅是他的一点贡献，葛立恒还在组合数学、图论、调度理论、计算机科学等诸多领域都做出过巨大贡献。
我们都听过所谓的“六度理论”，即任意两人之间都可以通过不超过6个人的人脉关系联系起来，这一理论恰恰是由葛立恒1979年的一篇论文发展而来。
而且，葛立恒不仅仅是一名数学家，还是一名杂技演员、魔术师。
传奇数学家
如果你不熟悉葛立恒，那一定会觉得他的名字非常特殊。
Graham通常翻译做格雷厄姆，为何Ronald Graham却翻译成了“葛立恒”这样一个有中国特色的名字？
原因是葛立恒有一位华人妻子金芳蓉。金芳蓉也是图论领域的专家，夫妻二人同是加州大学圣迭戈分校的数学教授。
葛立恒一生共发表350多篇论文和书籍，其中与妻子合作的就有90多篇。
谈到和葛立恒的婚姻，金芳蓉这样描述：
“许多数学家不愿嫁给同专业的人。他们担心二人之间会过于竞争。我们不仅都是数学家，而且都在同一领域工作。因此，我们可以理解和欣赏对方的工作，而且我们可以一起工作，有时会取得很好的进展。”
在生活中，葛立恒与另一位天才数学家保罗·埃尔德什（Paul Erdős）也有一段令人称颂的友谊，两人合作过30多篇论文。
 葛立恒夫妇与埃尔德什 葛立恒夫妇甚至还在家中留有一个专门的房间，给埃尔德什长期拜访居住。
由于埃尔德什比葛立恒大22岁，后来葛立恒还负责起埃尔德什的起居生活，包括管理收入、纳税还有帮他买衣服。
埃尔德什去世后，葛立恒负责打理由埃尔德什设立的奖金——埃尔德什奖，这笔奖金用于奖励那些解决某难题的青年才俊科学家，陶哲轩也曾获奖。
出生于1935年的葛立恒，于1962年获得了加州大学伯克利分校的博士学位，此后进入了AT&T的贝尔实验室工作，之后担任该实验室首席科学家。
在他的带领下，贝尔实验室建成了世界一流的离散数学和理论计算机科学研究中心。
在此期间，他曾在普林斯顿大学、斯坦福大学、加州理工学院、加州大学洛杉矶分校和戴维斯分校担任访问职位。葛立恒1999年被任命为加州大学圣迭戈分校的计算机与信息科学系主任。
2003年，葛立恒获得了美国数学学会颁发的斯蒂尔终身成就奖。
多才多艺的葛立恒，在此期间还有其他“副业”，他曾在1972年担任国际杂技演员协会主席。
葛立恒精通体操和蹦床，也是个会杂技的魔术师。
这些副业也给了他主业巨大的扶持。当葛立恒在研究数学问题受困时，他会在工作场所来一些杂耍动作放松头脑，获得灵感。
说到这里，你是否觉得葛立恒的人生已经足够开脑洞，而他最重要的葛立恒数才是把脑洞开到最大。
什么是葛立恒数
说到这里，我们进入烧脑环节。这个号称最大数的葛立恒数定义是这样的：
△ 图片引自waitbutwhy
为了搞清楚上面的标记到底是啥意思，我们先来介绍一个新的工具。
过去人们用科学记数法来表示大数实在是弱爆了，于是著名计算机学家高德纳想到了一个更好的办法。
没错，就是那位获得1974年图灵奖、还在写《计算机程序设计艺术》的计算机大神高德纳。
他提出的表示法被叫做高德纳箭头——通过不停给指数“套娃”的方式来构造大数。
一个高德纳箭头表示普通的指数：
3↑3 = 33 = 27
两个高德纳箭头表示指数嵌套的层数：
3↑↑3 = 3↑（3↑3）=3↑27 = 327 = 7625597484987
三个高德纳箭头是把二重箭头再算一遍：
3↑↑↑3 = 3↑↑（3↑↑3） = 3↑↑7625597484987 = ……
更直观的表示是这样的，总共嵌套了7625597484987层指数：
算到这里，3↑↑↑3已经是一个“天文”数字。算出它不可能，就是把它所有的指数写下来，也需要天文级别长度的纸条。
因为，如果我们每隔2厘米写一个3，那么得从地球写到太阳表面。
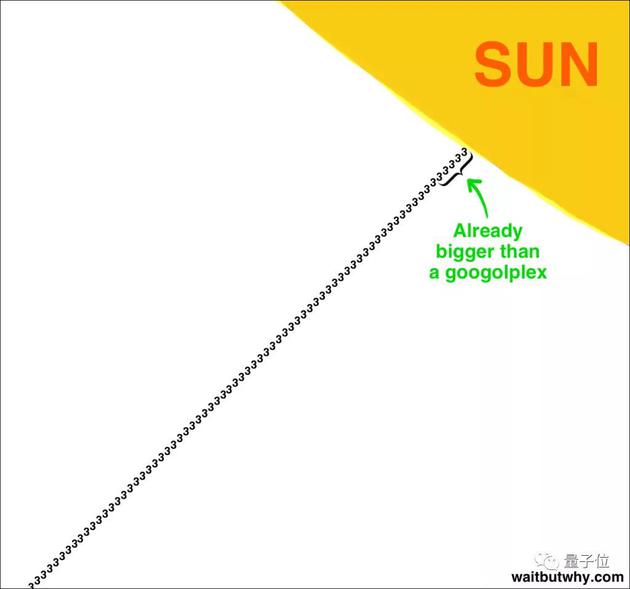 图片来源：waitbutwhy 四个高德纳箭头就是把三箭头再嵌套一次：
3↑↑↑↑3 = 3↑↑↑（3↑↑↑3） = 3↑↑↑（一个需要写到太阳的数） = ？？？
随着箭头的增长，数字的增长速度比指数函数不知道快多少倍。
然而这还仅仅是葛立恒数的第一层，也就是第二层的箭头数，第二层的数又是第三层的箭头数，……，葛立恒数这个“老千层饼”总共有64层。
这个数到底有多大？大到你的脑洞变成黑洞也装不下。
我们不仅没法算出来葛立恒数，甚至连葛立恒数位数的位数也无从知晓。
全宇宙的原子数量在葛立恒数面前就是0。假如你的脑子要装下葛立恒数，存储这个数的信息熵会大到让你的脑子变成黑洞。
至于葛立恒数的最后500位是这样的：
… 02425950695064738395657479136519351798334535362521430035401260267716226721604198106522631693551887803881448314065252616878509555264605107117200099709291249544378887496062882911725063001303622934916080254594614945788714278323508292421020918258967535604308699380168924988926809951016905591995119502788717830837018340236474548882222161573228010132974509273445945043433009010969280253527518332898844615089404248265018193851562535796399618993967905496638003222348723967018485186439059104575627262195195387
葛立恒数有什么用
为了防杠，在这里我们需要强调：比葛立恒数大的数还有无穷多个！
比如给葛立恒数加一、乘二，都能得到比它更大的数，但这些数字都没有具体的数学意义。
葛立恒数是有数学意义的最大数字（直到TREE（3）出现）。
那么，一个研究离散数学的人是怎样和巨大数字打起了交道？这要从葛立恒研究的图论说起。
葛立恒当年研究了拉姆齐理论中的一个问题：给n维立方体的边上色。我们先从最简单的二维立方体，也就是正方形说起。
正方形总有有4个顶点，把这些顶点全部两两连起来，总共会有6条线。这种把所有点全部连起来的图，在数学上叫做完全图。
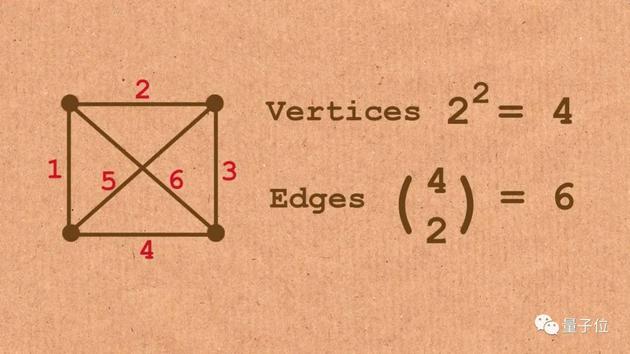 图片来源：YouTube @Numberphile 如果我们规定6条边只能涂上红蓝两种颜色，那么在一个平面里会不会有单色的完全图呢？
葛立恒在5年前的科普视频里告诉我们，在正方形上，确实可以找到一种涂色方法，可以不出现单色的完全图。
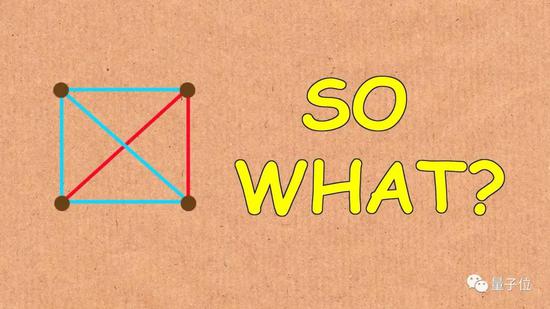 红色边所连3点没有构成完全图，因为底边是蓝色（来源同上） 那么到了3维情况会如何？立方体顶点间总共有28条连线，给它们按照以下方式上色。
你注意到了吗？有一个斜的平面中有个单色完全图，可是如果我们把最下面的边换成蓝色，那么就不能在任意一个平面内找到单色完全图了。
如果到4维、5维、6维……空间中的立方体，是不是存在一种涂色方法，让人找不到平面内的单色完全图呢？
通过具体的例子，我们发现2维、3维中立方体中，确实能找到这样的涂色方法、但是数学家们发现，当维度n大于一个数后，就再也找不到符合要求的涂色方法了。
至于n到底有多大，数学家到现在也没有完全证明，只能给出一个范围。
 数学家已经证明n≥13（来源同上） 而葛立恒证明，这个n最大不会超过葛立恒数。
《科学美国人》杂志的专栏作家Martin Gardner在大众科普中介绍了上述问题，葛立恒数的名称由此而来。
Gardner在文章里这样描述葛立恒数：
“其范围如此之大，以至是严肃数学证明中使用的最大数。”
虽然后来有更大的TREE（3）超越它，但是葛立恒数已经如此深入人心，以至于人们一提到最大数，首先就想到它。
今年我们已经失去了John Conway和葛立恒两位数学大师，令人惋惜。
斯人已逝，相信葛立恒已经和好友埃尔德什在另一个世界相聚。
如果寄托的哀思有一个数量限制的话，那一定是葛立恒数。
RIP |
